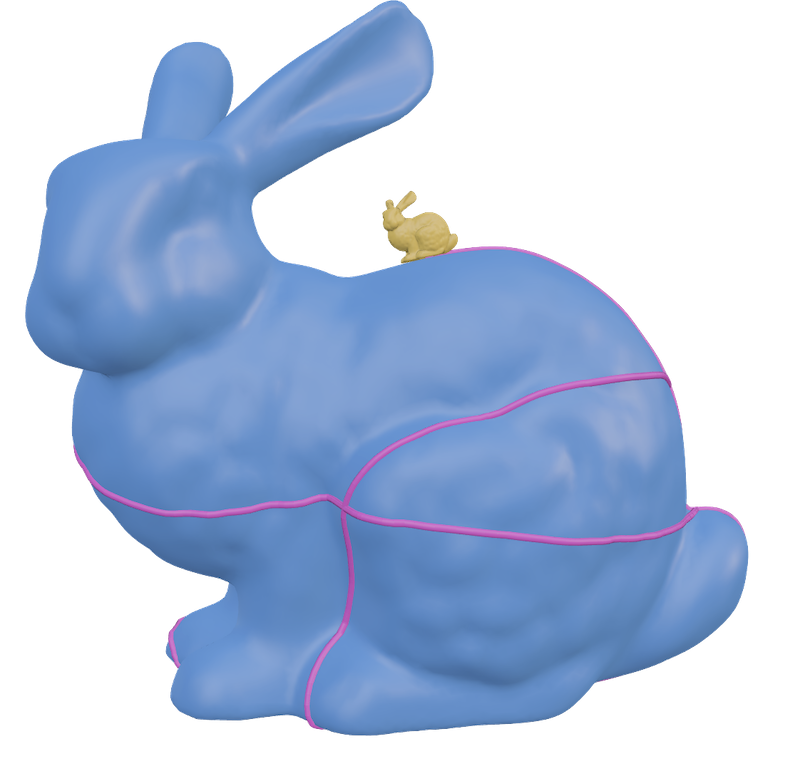
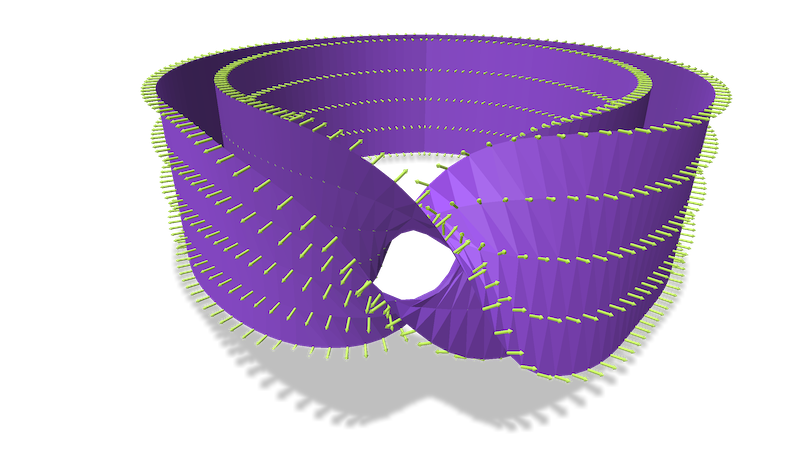
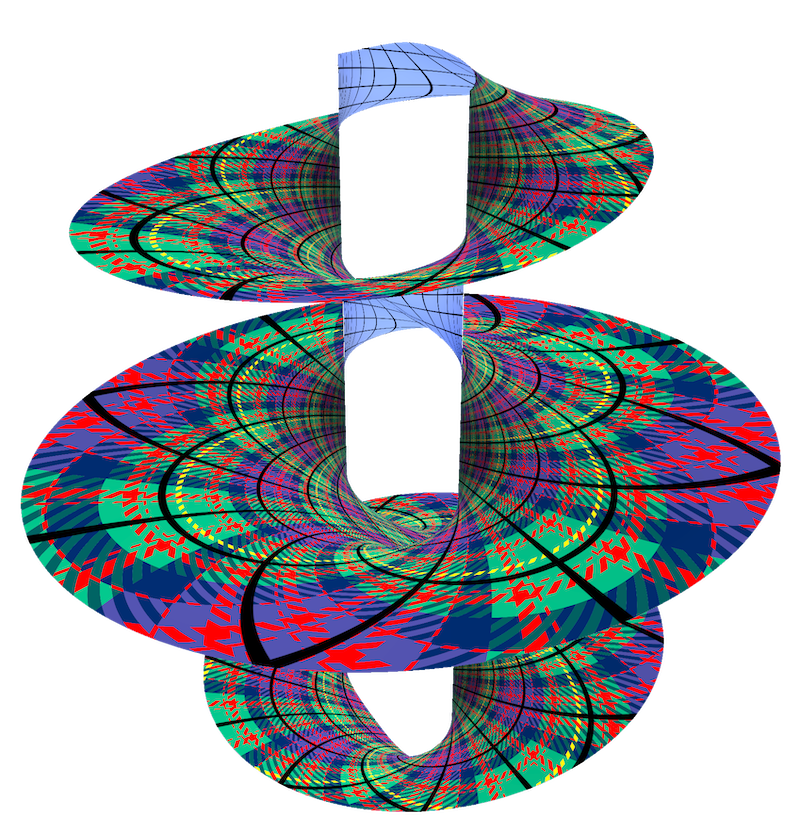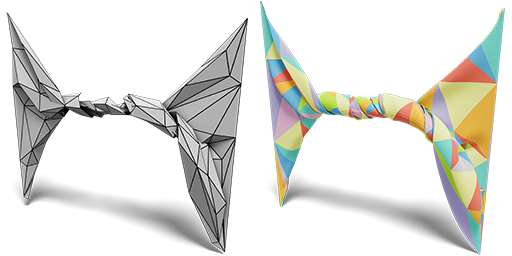I'm thrilled to be joining the University of Utah as an assistant professor in the Kahlert School of Computing in fall 2026. I'm looking for students to join my group—if you're excited about graphics and geometry processing and plan on applying to PhD programs this fall, please reach out!
I am currently a postdoc in computer science at École Polytechnique, working with Mathieu Desbrun. I design algorithms for reliably and efficiently processing geometric data, drawing inspiration from topology and differential geometry. I received my PhD from Carnegie Mellon University, where I was advised by Keenan Crane. Before that, I was an undergraduate at Caltech, where I worked on plasma simulation with Peter Schröder, chromosomal shape embeddings with Mathieu Desbrun, and interval analysis root finding techniques with Alan Barr.
In my spare time, I like to design origami models and knit.
News
- Jul. 2025This summer, I will be attending SGP in Bilbao and Siggraph in Vancouver. If you're planning on attending either one and want to meet up, let me know!
- Apr. 2024I accepted an assistant professor position at the University of Utah's Kahlert School of Computing! I will start in fall 2026.
- Dec. 2024I will serve on the program committee for the 2025 Symposium on Geometry Processing (SGP).
- Sept. 2024I started a postdoc with Mathieu Desbrun at École Polytechnique.
- Aug. 2024Ray Tracing Harmonic Functions and Solid Knitting were both awarded Best Paper Honorable Mentions at Siggraph 2024.
- May 2024I defended my PhD thesis at CMU.
- Aug. 2023I was invited to attend the geometry workshop in Obergurgl, which was relocated to Innsbruck due to flooding in Ötztal valley.
- Apr. 2019The National Science Foundation awarded me a Graduate Research Fellowship.
Research
Discrete connections are a staple of vector field design and analysis on meshes, but the notion of torsion of a discrete connection has remained unstudied. This is all the more surprising as torsion is a crucial ingredient of the smooth theory, underlying the fundamental theorem of Riemannian geometry. We extend the existing geometry processing toolbox by developing a theory of torsion for discrete connections.
Best Paper (Honorable Mention)
top 1.5% of accepted papers.
Sphere tracing is used throughout visual computing to render signed distance functions. We introduce an analogous algorithm for harmonic functions, opening up a range of possibilities: it can visualize point cloud reconstructions (via Poisson reconstruction) or polygon soups (via generalized winding numbers) without any linear solves or mesh extraction. We also show applications to Riemann surfaces, architectural grid shells, Seifert surfaces, and nonplanar polygons.
Best Paper (Honorable Mention)
top 1.5% of accepted papers.
Unlike standard knitting, which makes hollow surfaces, solid knitting creates dense volumes by layering knit sheets—much as 3D printers layer sheets of plastic. We envision a future where everyday objects like furniture or shoes can be knit in one piece. We define the basic building blocks of solid knitting and demonstrate a prototype solid knitting machine controlled by a low-level instruction language, along with a volumetric design tool for creating machine-knittable patterns.
My thesis develops algorithms and data structures for computing on surfaces whose geometry evolves over time. I take as examples the problems of mesh simplification and surface parameterization—in both cases, the intrinsic perspective leads to simple algorithms which are robust and efficient on a variety of challenging examples.
Winding numbers and their generalization to noisy data has proven invaluable in robust geometry processing. But standard definitions do not apply on surfaces, where not all curves bound regions. We develop a new generalization using the classic connections between winding numbers and harmonic functions.
We construct coarse intrinsic triangulations of an input surface. In the spirit of the quadric error metric (QEM), we perform greedy decimation while accumulating global error estimates. Rather than using extrinsic quadrics, however, we store intrinsic vectors that track how the mesh curvature drifts.
Integer coordinates provide a robust data structure for intrinsic triangulations of polyhedral surfaces. Our starting point is the framework of normal coordinates from geometric topology, which we extend to a broader set of operations needed for mesh processing. As a stress test, we successfully compute intrinsic Delaunay refinements and common subdivisions for all manifold meshes in the Thingi10k dataset.
Intrinsic triangulations decouple the mesh used to encode geometry from the mesh used for computation. The basic shift in perspective is to encode the geometry of a mesh not using vertex positions, but instead via edge lengths. This course provides an introduction to intrinsic triangulations and their applications, covering the theory, practical details, and some cutting-edge research in the area.
We present a new method for surface parameterization, leveraging hyperbolic geometry to find maps that are locally injective and discretely conformal in an exact sense. Stress tests involving difficult cone configurations and near-degenerate meshes indicate that the method is extremely robust in practice, providing high-quality interpolation even on meshes with poor elements.
Awards
| 2024 | Two SIGGRAPH Best Paper Award Honorable Mentions |
| Awarded to 12 papers out of about 840 submissions; ~1.5% of papers. | |
| 2019 | NSF Graduate Research Fellowship |
| Awarded to top 15% of applicants across all areas of science; $147,000 over 3 years. | |
| 2019 | Hertz Fellowship Finalist |
| Awarded to top 5% of applicants across applied science, math, and engineering. See here for details. | |
| 2017 | SIGGRAPH ACM Turing Award Celebration Grant |
| Awarded by SIGGRAPH to 10 students to attend the ACM Turing Award Celebration. | |
| 2017, 2016 | Arthur R. Adams SURF Fellowship |
| Summer research fellowship. |
Selected Talks
| May 2025 | Geometry Processing with Intrinsic Triangulations,GeomeriX Seminar, Inria Saclay |
| Apr. 2025 | Geometry Processing with Intrinsic Triangulations,CGAL Developer Meeting |
| pdf (25 mb) keynote file (240 mb) | |
| Apr. 2025 | Ray Tracing Harmonic Functions,CGAL Developer Meeting |
| pdf (28 mb) keynote file (1 gb) | |
| Feb. 2025 | New Foundations for Robust Geometry Processing,University of Utah |
| pdf (107 mb) keynote file (1.5 gb) | |
| Feb. 2025 | Ray Tracing Harmonic Functions,Oberwolfach Workshop on Mathematical Imaging and Surface Processing |
| video (30 min) pdf (31 mb) keynote file (1 gb) | |
| Nov. 2024 | Solid Knitting and Harmonic Hitting,Institute of Science and Technology Austria (ISTA) |
| pdf (38 mb) keynote file (1.7 gb) | |
| Aug. 2024 | Ray Tracing Harmonic Functions,ACM SIGGRAPH Technical Papers |
| video (10 min) | |
| Apr. 2024 | Evolving Intrinsic Triangulations,Carnegie Mellon University (CMU) |
| pdf (76 mb) keynote file (0.8 gb) | |
| Dec. 2023 | Dynamic Intrinsic Geometry Processing,Carnegie Mellon University (CMU) |
| pdf (79 mb) | |
| Sept. 2023 | Intrinsic Triangulations in Geometry Processing,Institute of Science and Technology Austria (ISTA) |
| Aug. 2023 | Intrinsic Triangulations in Geometry Processing,Geometry Workshop in Obergurgl |
| Jul. 2023 | Intrinsic Triangulations in Geometry Processing,TU Berlin SFB TRR 109 Colloquium |
| pdf (49 mb) | |
| Apr. 2022 | Discrete Conformal Equivalence of Polyhedral Surfaces,UCSD Pixel Cafe |
| pdf (32 mb) | |
| Mar. 2022 | Discrete Conformal Equivalence of Polyhedral Surfaces,Toronto Geometry Colloquium |
| pdf (19 mb) poster (8 mb) | |
| Dec. 2021 | Integer Coordinates for Intrinsic Geometry Processing,ACM SIGGRAPH Asia Technical Papers |
| video (20 min) video (5 min) | |
| Aug. 2021 | Discrete Conformal Equivalence of Polyhedral Surfaces,ACM SIGGRAPH Technical Papers |
| video (20 min) video (5 min) | |
| Oct. 2019 | Origami and Geometry,Carnegie Mellon University Graphics Lab |
| pdf (37 mb) | |
| Aug. 2021 | Geometry Processing with Intrinsic Triangulations,ACM SIGGRAPH 2021 Courses |
| video (3 hours) | |
| Jun. 2021 | Geometry Processing with Intrinsic Triangulations,SIAM IMR 2021 Courses |
Miscellanea
Web demo which traces out geodesics on a mesh. The code is available here.
Algorithm demonstrations on ShaderToy. Mostly from my paper on ray tracing harmonic functions.
Helper functions for tracing streamlines of vector/direction fields and generating textures for rendering them.
Notes on hyperbolic geometry and discrete conformal maps.
A shader to make meshes tartan.
GLSL implementation of BPM: Blended Piecewise Möbius Maps by Rorberg, Vaxman & Ben-Chen, incorporated into polyscope.
Takes any triangle mesh and turns it into an orientable manifold mesh by constructing the orientable double cover.
This is a rough implementation of the Delaunay edge split algorithm presented in Efficient construction and simplification of Delaunay meshes by Yong-Jin Liu, Chunxu Xu, Dian Fan, and Ying He. It takes in a triangle mesh and then performs edge splits to make the mesh Delaunay.
Web demo computing the Karcher mean of points on a sphere.
Visualization of the phase space of a pendulum as a cylinder.
Comparison of explicit, implicit, and symplectic Euler integrators for a pendulum.
Demo of an implementation of the combinatorial map data structure for n-dimensional simplicial complexes that I experimented with in geometry-central. It has not yet made its way into the library itself, but the implementation can be found here.
Online tool to check if a word is in the dictionary.
