Milnor's Lobachevsky Function ($\text{Л}$)

\[\text{Л}(x) := -\int_0^x \log \left| 2 \sin t\right|\;dt\]

Note that \[\begin{aligned} \text{Л}'(x) &= - \log |2 \sin x| \\ \text{Л}''(x) &= -\cot x \end{aligned}\]

The definition looks very strange. It's probably easiest to think of Л as being defined by the differential equation \[ \text{Л}''(x) = -\cot x \] subject to the initial conditions \[\begin{aligned} \text{Л}(0) &= 0\\ \text{Л}'\left(\frac \pi 2\right) &= 0\\ \end{aligned}\]

Useful Facts

A Circumradius Forumla

We begin with a seemingly-unrelated formula about the circumcircle of a triangle.

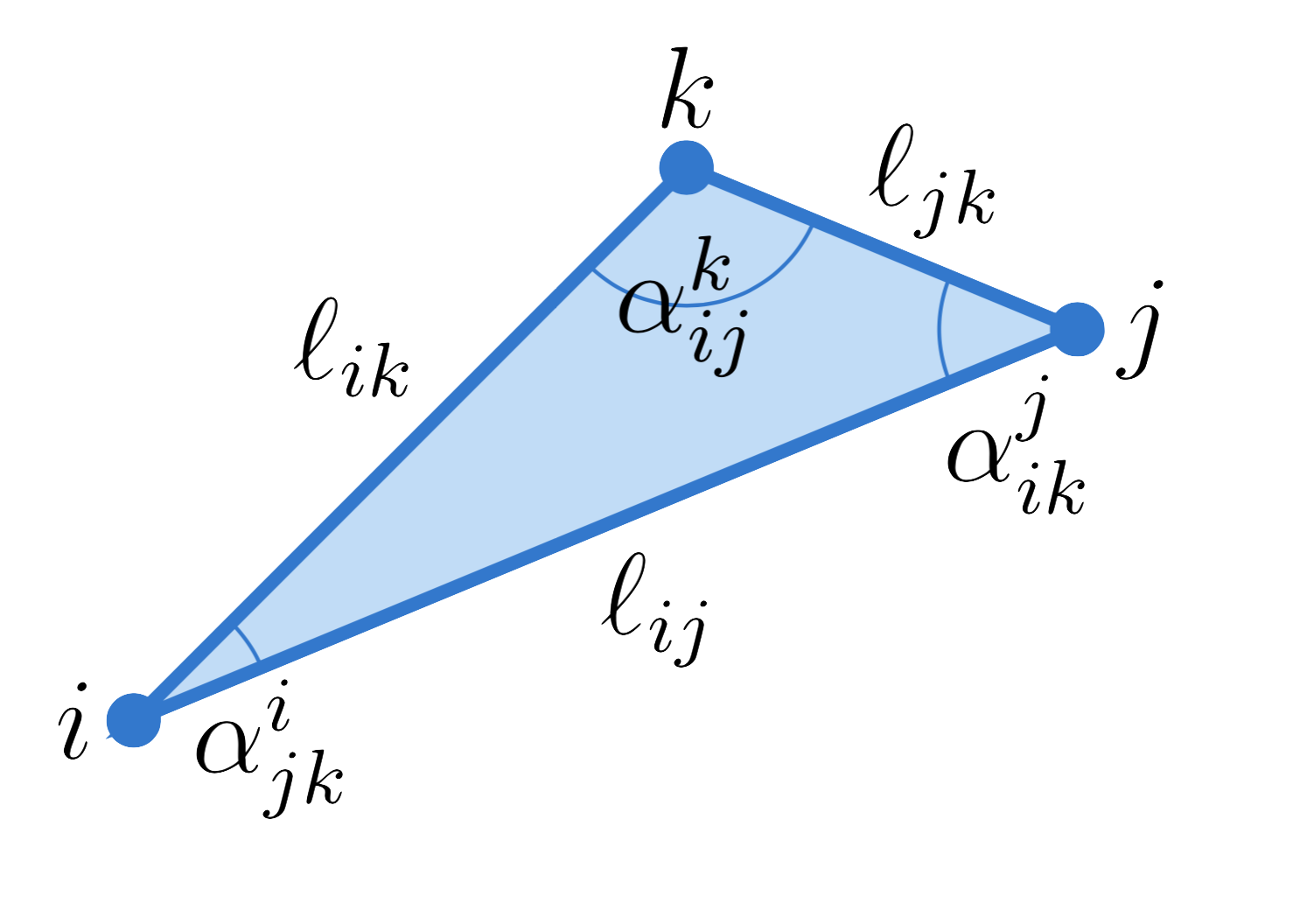
Let $t_{ijk}$ be a triangle with edge lengths $\ell_{ij}, \ell_{jk}, \ell_{ki}$ and angles $\alpha_{ij}^k, \alpha_{jk}^i, \alpha_{ki}^j$.
The radius of the circumcircle of $t_{ijk}$ is given by $R = \frac{\ell_{jk}}{2 \sin \alpha_{jk}^i}$.
Proof

We place our triangle inside of its circumcircle.

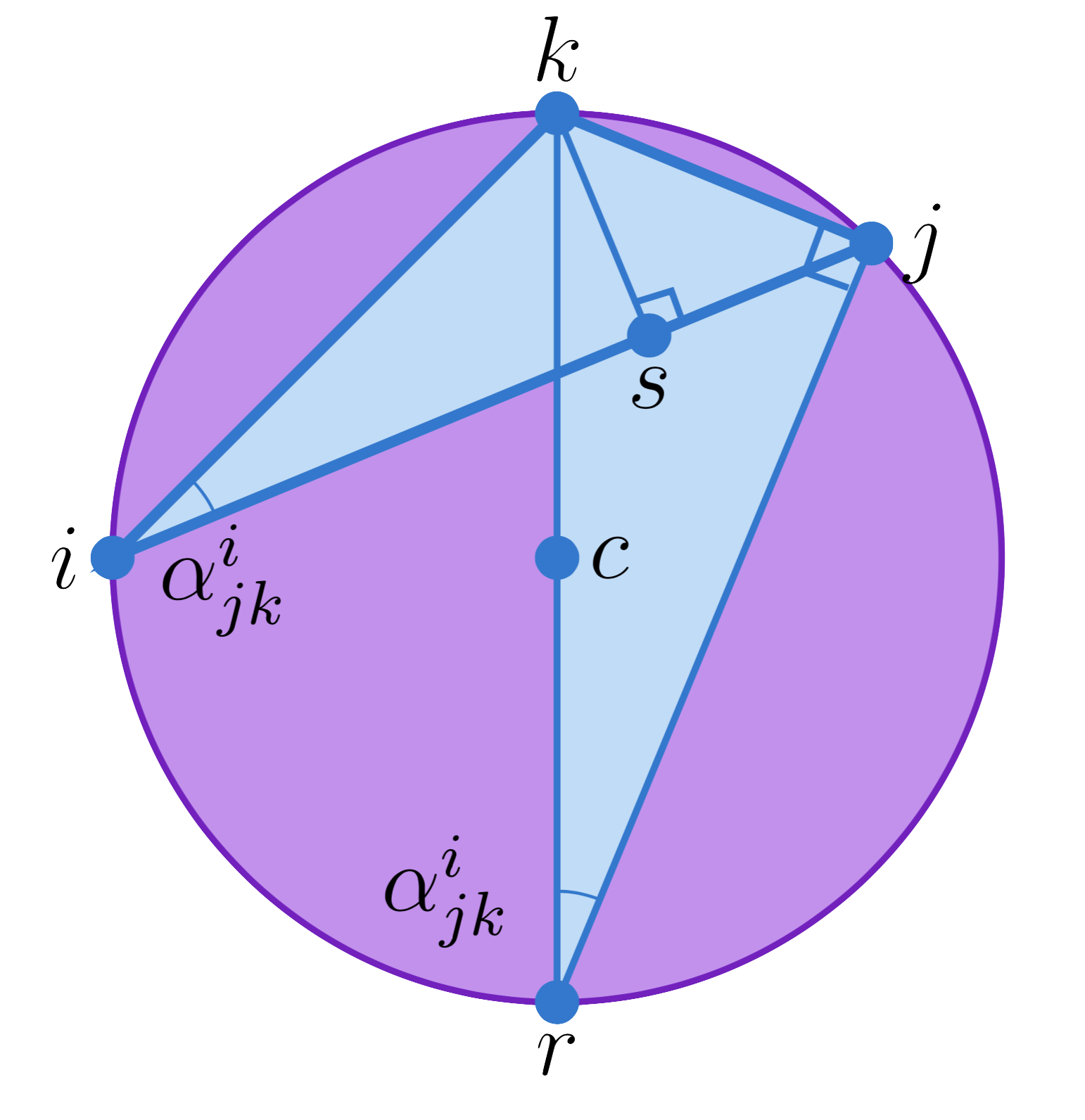
$c$ is the center of the circle. We draw a diagonal passing though $k$, and name the opposite point $r$. Note that angle $k-j-r$ must be a right angle, since the line $\overline{kr}$ is a diameter of the circle. We also place a point $s$ such that the angle $k-s-j$ is a right angle.

Note that angle $k-r-j$ must equal angle $\alpha_{jk}^i$ since both subtend the same arc between $k$ and $j$. Therefore, triangle $t_{isk}$ is similar to triangle $t_{rjk}$. In particular, this means that \[\frac {\ell_{kr}}{\ell_{kj}} = \frac {\ell_{ik}}{\ell_{sk}}\] Note that $\ell_{sk} = \ell_{ik} \sin \alpha_{jk}^i$. Furthermore, $\ell_{rk} = 2R$. Thus, we see that \[\frac {2R}{\ell_{kj}} = \frac {\ell_{ik}}{\ell_{ik} \sin \alpha_{jk}^i}\] Simplifying, we conclude that \[R = \frac{\ell_{jk}}{2\sin\alpha_{jk}^i}\]

Energy Derivative

Futhermore, let $\lambda_{mn} = 2 \log \ell_{mn}$. We define a function \[ f( \lambda_{ij}, \lambda_{jk}, \lambda_{ki}) = \frac 12 \big( \alpha_{jk}^i \lambda_{jk} + \alpha_{ki}^j \lambda_{ki} + \alpha_{ij}^k \lambda_{ij}\big) + \text{Л}( \alpha_{jk}^i) + \text{Л}( \alpha_{ki}^j) + \text{Л}( \alpha_{ij}^k) \]
\[\pd f {\lambda_{jk}} = \frac 12 \alpha_{jk}^i\]
Proof

Using the circumradius formula, this becomes a straightforward computation.

\[\begin{aligned} \pd f {\lambda_{jk}} &= \frac 12 \alpha_{jk}^i + \left(\frac 12\lambda_{jk} - \log |2 \sin \alpha_{jk}^i| \right) \pd {\alpha_{jk}^i}{\lambda_{jk}}\\ &\quad+ \left(\frac 12\lambda_{ki} - \log |2 \sin \alpha_{ki}^j| \right) \pd {\alpha_{ki}^j}{\lambda_{jk}} + \left(\frac 12 \lambda_{ij} - \log |2 \sin \alpha_{ij}^k| \right) \pd {\alpha_{ij}^k}{\lambda_{jk}}\\ &= \frac 12 \alpha_{jk}^i + \log\left(\frac {\ell_{jk}}{2 \sin \alpha_{jk}^i}\right) \pd {\alpha_{jk}^i}{\lambda_{jk}} + \log\left(\frac {\ell_{ki}}{2 \sin \alpha_{ki}^j}\right) \pd {\alpha_{ki}^j}{\lambda_{jk}} + \log\left(\frac {\ell_{ij}}{2 \sin \alpha_{ij}^k}\right) \pd {\alpha_{ij}^k}{\lambda_{jk}} \end{aligned}\] By the circumradius formula, each of those log terms is just $\log R$. (Equivalently, we could just use the law of sines here to observe that all of the terms are equal. It is not actually important what they are equal to). Thus, we have \[\begin{aligned} \pd f {\lambda_{jk}} &= \frac 12 \alpha_{jk}^i + \log R \pd{}{\lambda_{jk}} \left(\alpha_{jk}^i + \alpha_{ki}^j + \alpha_{ij}^k\right) \end{aligned}\] Since the sum of the angles in a triangle is always $\pi$, the derivative on the right vanishes. Thus, we obtain the desired equality \[\begin{aligned} \pd f {\lambda_{jk}} &= \frac 12 \alpha_{jk}^i \end{aligned}\]